Events
- 2018
-
Speaker
Rosalba García-Millán( Imperial College, London, UK)Description
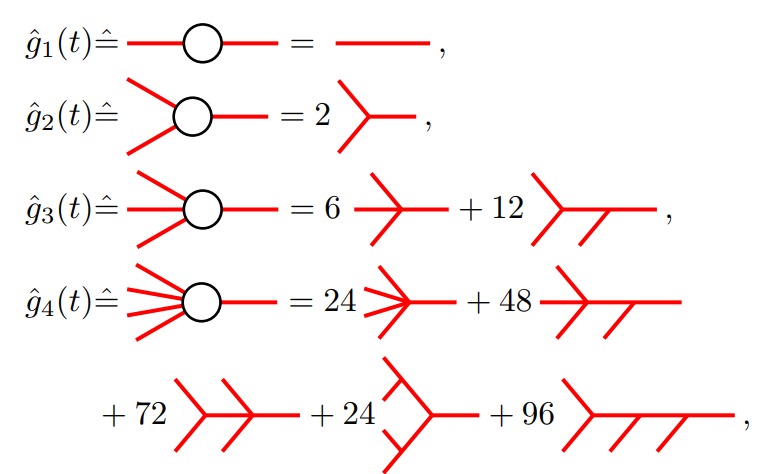
Braching processes have been widely studied and applied to model phenomena such as gambling, percolation and avalanching. In my talk, I will present our field-theoretic approach to continuous-time branching processes, a method that allows us to calculate new observables such as the temporal scaling of the moments of the instant population size, the so-called avalanche shape, the n-point correlation function and the probability density function of the total avalanche size. This is joint work with Johannes Pausch, Benjamin Walter and Gunnar Pruessner (preprint arXiv:1808.08418).
-
Speaker
Guillermo GarcíaDescription
Thesis defense. Advisors: Prof. M. Ángeles Serrano and Dr. Marián Boguñá.
-
Speaker
Dominik Lips and Philipp Maass (Department of Physics, Osnabrück University, Germany)Description
Models of driven stochastic particle transport in one dimension have been applied to describe such diverse phenomena as biopolymerization, molecular motor motion along filaments, flow of molecules through nanopores, ion conduction through membrane channels, electron transport along molecular wires, and vehicular traffic. A simple lattice model, the asymmetric simple exclusion process (ASEP) appears as a basic building block in the theoretical description of these driven diffusion systems and has developed into one of the standard models for investigating non-equilibrium steady states. After an introduction to the physics of the ASEP and some model variants with the focus on non-equilibrium phase transitions [1-3], we address the question whether corresponding phenomena will occur in driven Brownian motion, making them more amenable to experimental studies.
Specifically, we introduce a model of a Brownian asymmetric simple exclusion process (BASEP) with overdamped Brownian dynamics and a setup resembling that of the ASEP on a lattice [4]. In this BASEP, particles of size σ with hardcore interaction are driven by a constant drag force through a cosine potential with period λ and an amplitude much larger than the thermal energy.
We show that the character of the non-equilibrium steady states in the BASEP is strikingly different from that in the ASEP. Compared with a system of non-interacting particles, the current is enhanced for small σ/λ ratios due to a barrier reduction effect arising from multi-occupation of potential wells. Larger σ/λ ratios lead to a suppression of the current because of blocking effects. Surprisingly, an exchange- symmetry effect causes the current-density relation to be identical to that of non- interacting particles for commensurable lengths σ=nλ, n=1,2... A behavior similar as for the ASEP is obtained only in a limited parameter regime. The rich behavior of the current-density relation leads to phase diagrams of non-equilibrium steady states with up to five different phases. The structure of these phase diagrams changes with varying σ/λ ratio.
[1] M. Dierl, P. Maass, and M. Einax, Phys. Rev. Lett. 108, 060603 (2012).
[2] M. Dierl, M. Einax, and P. Maass, Phys. Rev. E 87, 062126 (2013).
[3] M. Dierl, W. Dieterich, M. Einax, and P. Maass, Phys. Rev. Lett. 112, 150601 (2014).
[4] D. Lips, A. Ryabov, and P. Maass, Phys. Rev. Lett. 121, 160601 (2018).
-
Description
La xarxa d'Internet, les xarxes d'amistat a les escoles, els insectes socials i els organismes són exemples de sistemes complexos que es basen no només en les propietats intrínseques dels components (reduccionisme), sinó també en les interaccions entre els seus components. Entendre l'origen de la complexitat és un aspecte fonamental per tractar els desafiaments del món actual. Un dels aspectes clau d'aquests sistemes es troba en la dificultat que hi ha amb la modelització i simulació computacional i que necessita un enfocament purament multidisciplinari i integrador de moltes disciplines del coneixement. En aquest curs farem una introducció als sistemes complexos i les eines bàsiques per tal d’analitzar-los, emfatitzant en la descripció necessàriament interdisciplinar.
Objectius
El principal objectiu és fer arribar als docents de secundària de diferents matèries el tipus de sistemes que s’estudien dins el marc del que avui en dia anomenem ciència dels sistemes complexos. Aquesta ciència, que no es pot associar de manera immediata a cap de les ciències que podríem anomenar dins la classificació “tradicional”, és per definició interdisciplinària, ja que integra successives escales de definició que pertanyen a les disciplines tradicionals. Una ciència que ens permet passar de la descripció de la cel·la als òrgans, als organismes i a les poblacions. De les interaccions entre neurones al cervell i d’aquí a la psicologia i a les xarxes socials. També de com d’importants són les matemàtiques per una correcte descripció d’aquest món i les noves eines computacionals.
Programa
8.45 – 9.00h
Acollida
9.00 – 9.15h
Presentació de complexitat.CAT.
Álvaro Corral Cano, president
9.15 – 10.00h
Introducció als sistemes complexos.
Albert Diaz Guilera, catedràtic de Física de la Matèria Condensada de la UB i director de l’Institute of Complex Systems (UBICS)
10.00 – 11.00h
Principis: Emergència i autoorganització.
Sergi Valverde, professor lector a la UPF i membre del Complex Systems Lab
11.00 – 11.30h
Cafè i Networking.
11.30 – 12.30h
Patrons de la complexitat: Fractals.
Sergi Valverde
12.30 – 13.30h
Fonaments educatius de les xarxes complexes.
Gemma Rosell, investigadora predoctoral al Complexity Lab Barcelona (ClabB) i membre del UBICS
13.30 – 14.00h
Ronda de preguntes als ponents i cloenda.
Destinataris: Personal docent de secundària interessat en la interdisciplinarietat
Se certificaran: 5 hores.
Places: 50
Preu: 10€
Període inscripció: del 30 de juliol al 2 de novembre de 2018.
Inscripció per Internet: Formulari de matrícula
Informació i consultes
A/e: icecursos@ub.edu
Tel.: 934 021 024Organizers
complexitat.cat (http://complexitat.cat) -
Speaker
Gorka Zamora-López (Center for Brain and Cognition, UPF)Description
Discovered in the realm of social sciences the small-world phenomenon stands for the observation that any two individuals are connected by a short chain of social ties. Since then, most real networks studied have been found to be small-world as well. Despite its significance to understand empirical networks, a quantitative determination of "how short" or "how long" a network is, and how it compares to others has remained unresolved over the years. When we say that “a complex network is small-world” we mean, roughly speaking, that its average path-length is much smaller than the number of nodes, without giving further precise measurement. The usual strategy to deal with this problem has been to compare networks to well-known graph models, e.g., random graphs and regular lattices. While these represent interesting null-hypotheses, useful to answer particular questions about the data, they do not constitute absolute or universal references. Here, we establish a reference framework under which the length and efficiency of networks can be interpreted and compared. Therefore, we will evaluate how these properties deviate from the smallest and the largest values they could possibly take. We have found that these limits are given by families of singular configurations which we will refer as ultra-short and ultra-long networks. We show that typical models (random, scale-free and ring networks) undergo a transition as their density increases, all becoming ultra-short at sufficient density. The convergence rate, however, differs for each model. Then, we study a sample set of well-known empirical networks (neural, social and transportation). While most of these display path-lengths close to random graphs, when contrasted against the absolute boundaries, only the cortical connectomes reveal quasi-optimal.
